DenseNet:Densely Connected Convolutional Networks
10 Mar 2020 | Deep learning Object detection DenseNetDenseNet
DenseNet은 2017 CVPR 컨퍼런스에 Densely Connected Network라는 네트워크 구조에 획기적인 변화를 주는 CNN 모델이 발표됐습니다. ResNet의 skip connection과 다른 Dense connectivity를 제안했습니다. 이 모델의 장점으로는 이미지에서 저수준의 특징들이 잘 보존되고, gradient가 수월하게 흘러 gradient vanishing 문제(1)가 발생하지 않으며, 깊이에 비해 파라미터 수가 적기에 연산량이 절약됨과 동시에 적은 데이터셋에서도 비교적 잘 학습이 된다는 점이 있습니다.
Dense connectivity
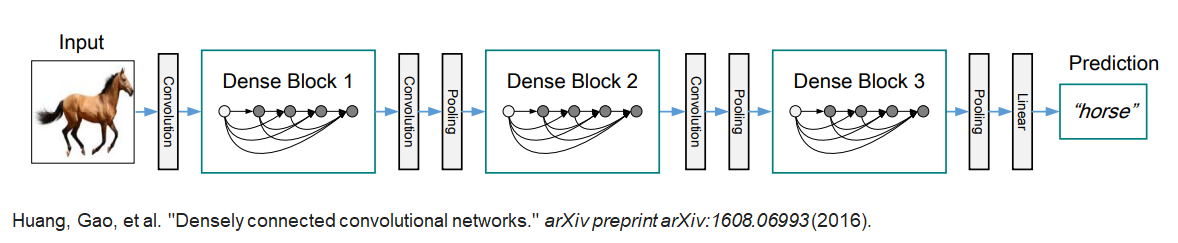
DenseNet의 핵심은 Dense connectivity 입니다. Dense connectivity란, 입력값을 계속해서 출력값의 채널 방향으로 합쳐주는 것(Concat)입니다.
즉, 이전 layer들의 feature map을 계속해서 다음 layer의 입력과 연결하는 방식이며 이러한 방식은 ResNet에서도 사용이 되었습니다. 다만 ResNet은 feature map 끼리 더하기를 해주는 방식이었다면 DenseNet은 feature map끼리 Concatenation을 시키는 것이 가장 큰 차이점입니다.
이를 ResNet과 수식으로 비교하면 다음과 같습니다.
ResNet의 경우에는 입력이 출력에 더해지는 것이기 때문에 종단에 가서는 최초의 정보가 흐려질 수 밖에 없습니다. 그에 반해 DenseNet의 경우에는 채널 방향으로 그대로 합쳐지는 것이기 때문에 최초의 정보가 비교적 온전히 남아있게 됩니다.
DenseNet의 구조: DenseNet-121
| 유형 | 입력 크기 | 출력 크기 | 커널 크기 | 횟수 |
|---|---|---|---|---|
| 입력 | (224,224,3) | |||
| Conv | (224,224,3) | (112,112,64) | (7,7) | |
| maxpool | (112,112,64) | (56,56,64) | (3,3) | |
| Dense Block | (56,56,64) | (56,56,256) | $\begin{bmatrix} 1\times1,128 \ 3\times3,32 \end{bmatrix}\;\;$ | $\times 6$ |
| Conv | (56,56,256) | (56,56,128) | (1,1) | |
| Average pool | (56,56,128) | (28,28,128) | (2,2) | |
| Dense Block | (28,28,128) | (28,28,512) | $\begin{bmatrix} 1\times1,128 \ 3\times3,32 \end{bmatrix}\;\;$ | $\times 12$ |
| Conv | (28,28,512) | (28,28,256) | (1,1) | |
| Average pool | (28,28,256) | (14,14,256) | (2,2) | |
| Dense Block | (14,14,256) | (14,14,1024) | $\begin{bmatrix} 1\times1,128 \ 3\times3,32 \end{bmatrix}\;\;$ | $\times 24$ |
| Conv | (14,14,1024) | (14,14,512) | $1\times1,512$ | |
| Average pool | (14,14,512) | (7,7,512) | (2,2) | |
| Dense Block | (7,7,512) | (7,7,1024) | $\begin{bmatrix} 1\times1,128 \ 3\times3,32 \end{bmatrix}\;\;$ | $\times 16$ |
| Average pool | (7,7,1024) | (1,1,1024) | (7,7) | 1 |
| FCN | (1,1,2048 | (1,1,1000) | ||
| softmax | (1,1,1000) | (1,1,1000) |
첫번째 convolution과 maxpooling 연산은 ResNet과 똑같습니다. 이 후 Dense Block과 Transition layer가 반복되고, 마지막의 fully connected layer와 softmax로 예측을 수행합니다.
Dense Block
Dense connectivity를 적용하기 위해서는 feature map의 크기가 동일해야합니다. 같은 feature map 크기를 공유하는 연산을 모아서 Dense Block을 구성하고 이 안에서 Dense connectivity를 적용합니다. 이 때, ResNet에서 배웠던 Bottleneck Layer를 사용합니다.
Growth Rate
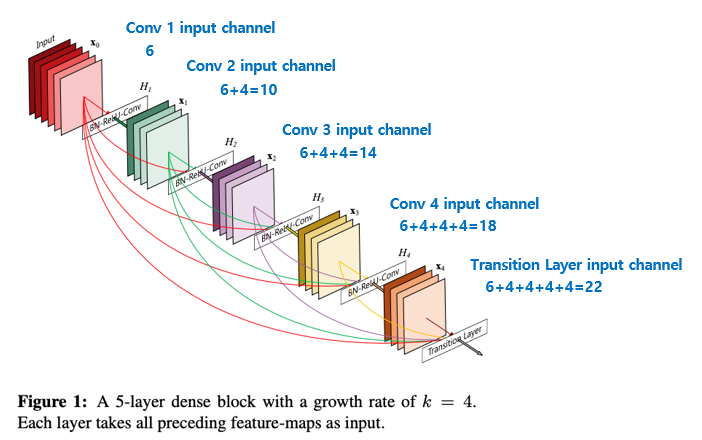
각 feature map끼리 dense하게 연결되는 구조이다 보니 자칫 feature map의 channel 개수가 많은 경우 계속해서 channel-wise로 concat이 되면서 channel이 많아 질 수 있습니다. 그래서 DenseNet에서는 각 layer의 feature map의 channel 개수를 굉장히 작은 값을 사용하며, 이 때 각 layer의 feature map의 channel 개수를 growth rate(k) 이라 부릅니다.
위의 fig1 그림은 k(growth rate) = 4 인 경우를 의미하며 fig1의 경우로 설명하면 6 channel feature map 입력이 dense block의 4번의 convolution block을 통해 (6 + 4 + 4 + 4 + 4 = 22) 개의 channel을 갖는 feature map output으로 계산이 되는 과정을 보여주고 있습니다. 위의 그림의 경우를 이해한다면 실제 논문에서 구현한 DenseNet의 각 DenseBlock의 각 layer마다 feature map의 channel 개수 또한 간단한 등차수열로 나타낼 수 있습니다.
Bottleneck Layer
ResNet과 Inception 등에서 사용되는 bottleneck layer의 아이디어는 DenseNet에서도 찾아볼 수 있습니다.
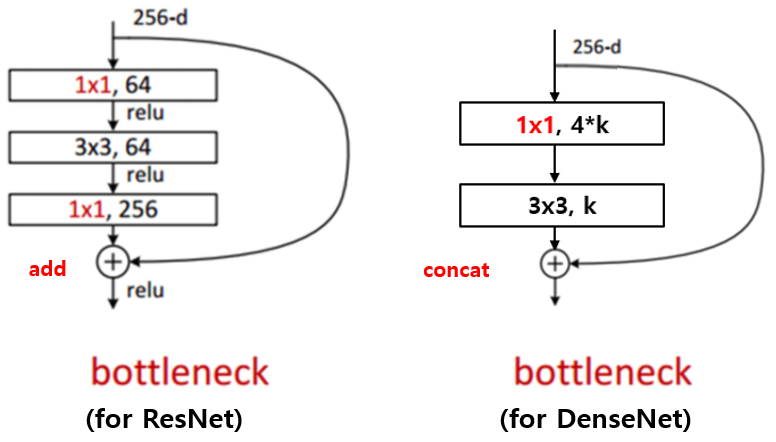
3x3 convolution 전에 1x1 convolution을 거쳐서 입력 feature map의 channel 개수를 줄이는 것 까지는 같은데, 그 뒤로 다시 입력 feature map의 channel 개수 만큼을 생성하는 대신 growth rate 만큼의 feature map을 생성하는 것이 차이 점이며 이를 통해 computational cost를 줄일 수 있다고 합니다.
또한 구현할 때 약간 특이한 점이 존재합니다. DenseNet의 Bottleneck Layer는 1x1 convolution 연산을 통해 4*growth rate 개의 feature map을 만들고 그 뒤에 3x3 convolution을 통해 growth rate 개의 feature map으로 줄여주는 점이 특이합니다. Bottleneck layer를 사용하면, 사용하지 않을 때 보다 비슷한 parameter 개수로 더 좋은 성능을 보임을 논문에서 제시하고 있습니다.
다만 4 * growth rate의 4배 라는 수치는 hyper-parameter이고 이에 대한 자세한 설명은 하고 있지 않습니다.
Transition Layer
Dense Block 사이에 있는 1x1 convolution 연산과 average pooling 연산을 묶어 Transition layer 라고 합니다. 이 layer는 feature map의 가로, 세로 사이즈를 줄여주고 feature map의 개수를 줄여주는 역할을 담당하고 있습니다. Batch Normalization, ReLU, 1x1 convolution, 2x2 average pooling 으로 구성이 되어있습니다.
1x1 convolution을 통해 feature map의 개수를 줄여주며 이 때 줄여주는 정도를 나타내는 theta 를 논문에서는 0.5를 사용하였으며 마찬가지로 이 값도 hyper-parameter입니다. 이 과정을 Compression이라 논문에서 표현하고 있습니다. 즉 논문에서 제시하고 있는 transition layer를 통과하면 feature map의 개수(channel)이 절반으로 줄어들고, 2x2 average pooling layer를 통해 feature map의 가로 세로 크기 또한 절반으로 줄어듭니다. 물론 theta를 1로 사용하면 feature map의 개수를 그대로 가져가는 것을 의미합니다.
Implementation details
본 논문에서는 ImageNet, CIFAR-10, SVHN 3가지 데이터셋에 대해 실험을 하였으며, ImageNet은 다른 두가지 데이터셋에 비해 이미지 사이즈가 크기 때문에 ImageNet과 나머지 두 데이터셋이 다른 architecture를 가지는 것이 특징입니다.
Additional
(1) Gradient Vanishing problem
Gradient Vanishing 문제란 0과 1사이의 값을 가지는 sigmoid function에서 아주 작은
값을 가질 경우 0에 매우 가까운 값을 가지게 됩니다. ex)0.00001
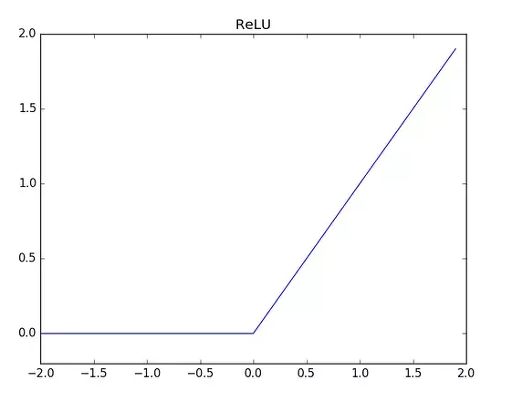
Gradient Descent를 사용해 Back-propagation 시 각 layer를 지나며 이를 지속적으로 곱해주게 되는데요. 이때 layer가 많을 경우에는 결국 0으로 수렴하는 문제가 발생합니다. 주로, ReLU를 사용함으로써 Gradient Vanishing 문제를 해결할 수 있습니다.
Reference
[1] Densely Connected Convolutional Networks, 2016 [paper]
https://datascienceschool.net/view-notebook/4ca30ffdf6c0407ab281284459982a25/
https://ydseo.tistory.com/41
https://jayhey.github.io/deep%20learning/2017/10/13/DenseNet_1/

 Hyojin Kim's blog
Hyojin Kim's blog